

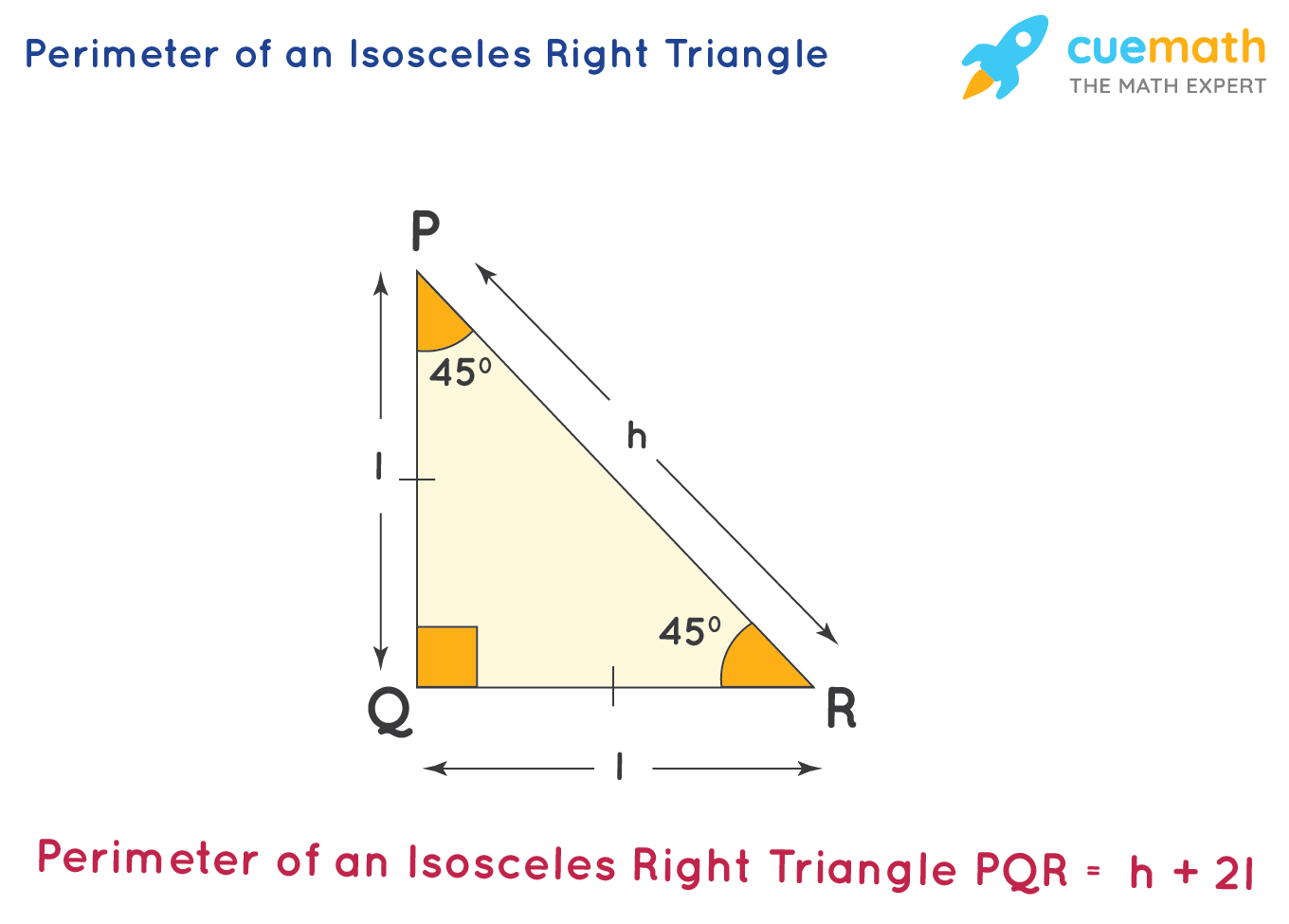
The cases where AB=AC (blue), AB=BC (red), and AC=BC (green) (lighter versions on the left side of the y-axis) are shown below for measures of angle C between 0 and 180°. Examples of isosceles triangles include the isosceles right triangle. Mangaldan's comment), and by symmetry this perpendicular bisector of AB also bisects $\angle ACB$ from there, you can use right triangle trigonometry to determine the coordinates of C (left for you to solve). In geometry, an isosceles triangle is a triangle that has two sides of equal length. In the third case, C is equidistant from A and B, so C must lie on the perpendicular bisector of AB (as in J. Find Right Triangle stock images in HD and millions of other royalty-free stock photos, illustrations and vectors in the Shutterstock collection. And so, if we have two triangles where two of the angles are the same, we know. And so, and if we drop an altitude right over here which is the whole point, that's the height, we know that this is, these are going to be right angles. And so, these base angles are also going to be congruent. Finally, solve the equation to find the unknown base, x. Then, use the Pythagorean theorem to create an equation involving x. The second case is similar to the first (so it's left for you to solve). An isosceles triangle has two sides that are the same. A right triangle has one 90° angle and a variety of often-studied topics: Pythagorean Theorem. To find the value of a base (x) in an isosceles triangle, first split the triangle into two congruent right triangles by drawing an altitude. Edit (to match revised question): Given your revised question, there is still the issue of C being on either side of the y-axis, but you have specified that AB=AC and that you are given $\mathrm\angle C))$. Right angle In a right triangle ABC with a right angle at the apex C.


 0 kommentar(er)
0 kommentar(er)
